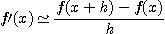기본 수치 해석

수치미분  및  수치적분

 

목적: 1. 미분방정식의 수립을 위한 수치 미분법
        2. 임의의 함수의 적분법
            가. Gaussian Quadrature
            나. Monte Carlo Integral

 1. 수치 미분법

가) 가장 기본적인 미분법

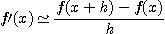     이다.

이러한 수치 미분의 오차의 크기는

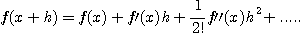    에서

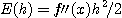    가 된다.

나) 보다 나은 미분법

    
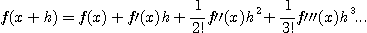
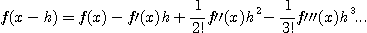     등으로 부터

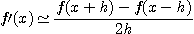     (오차는 )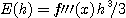

이 된다.

다) 2 계 미분법

    
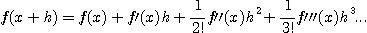
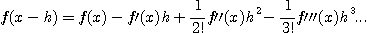     등으로부터

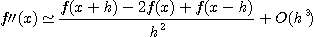
2. 임의의 함수의 적분법

  가. Gaussian Quadrature

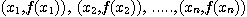       을 알 때 적분법

a) Trapezoidal Rule(사다리 꼴 공식)

     이웃 하는 두 점 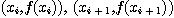사이를 직선으로 연결한다음 적분

      즉

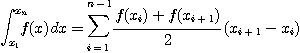
을 이용해 수치 적분 하면 된다.

b) Simpson's Rule

      이웃 하는 세 점 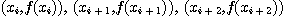을 포물선으로 연결한 다음 적분. 특히 임의의 이웃하는 두 점의 x 좌표의 차가

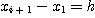
      와 같이 일정할 때에는 Simpson's Rule은

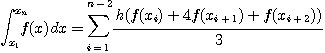
을 이용해 수치 적분 하는 것을 의미한다. 따라서 이 때에는 적분 구간 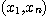을 홀수개의 점으로 분할하는 것이 좋다.

c) Simpson의 3/8 Rule

     이웃 하는 4 점 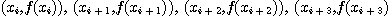을 삼차식 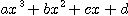으로 연결한 다음 적분. 특히 임의의 이웃하는 두 점의 x 좌표의 차가

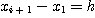
      와 같이 일정할 때에는 Simpson's 3/8 Rule은

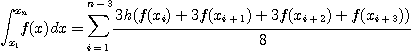
을 이용해 수치 적분 하는 것을 의미한다. 이 때에는 적분 구간 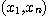을 (3K+1) 개의 점으로 분할하는 것이 좋다.

3. Numerical Intergral의 구현

    수치 적분 하는 프로 그램 한 example을 보여 보자. 우선 프로 그램이 시작되면 다음 그림과 같은

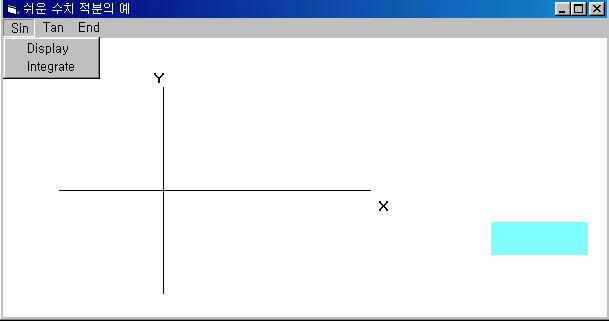
form이 열리고 menu 중 Sin-Display를 열면 우리가 이미 공부한 기초 전산 그리기에서와 같은 sine함수가 -Pi에서 +2Pi까지 그려진다. 그 다음 menu 중 Sin-Intergrate를 열면 정적분의 상한 하한을 대화 상자를 이용해 입력하게 된다. 그 그림은 다음과 같다.

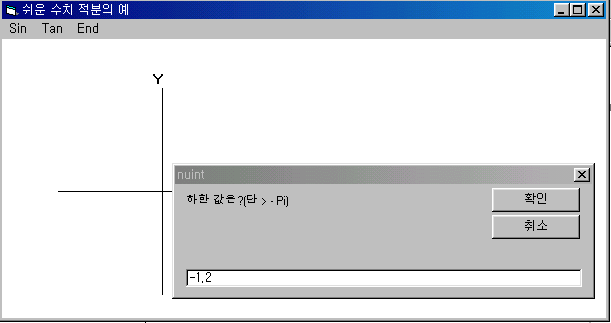
이제 상한 하한을 입력하면 적분을 하는 구간을 푸른 색으로 표시하고 그 적분 값을 표시하는 label box에 표시한다. 그 결과는 다음 그림과 같다.

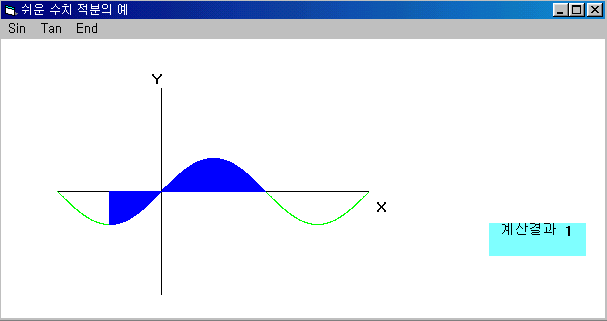
이러한 프로그램의 project file, form file, 및 실행file은 각각 nuint.vbp, nuint.frm. nuint.exe에 각각 있다. 이제 이 프로 그램의 form을 구성하는 여러 control들의 속성 표를 작성해 보자. 속성표는 먼저 Menu Editor에서 Menu를 작성하는데 그 Menu 구성도는 다음과 같다.

그 다음의 속성표는 모두 기초 전산 그리기의 프로그램 예인 sine.vbp와 sine.frm의 경우와 동일한데 다만 결과를 나타내는 label box인 lblresult가 더 추가 되어 있다. Menu Sin-Display를 Click했을 때와 Menu End를 Click했을 때 수행되는 프로그램 source code는 sine.vbp와 sine.frm와 동일하다. 이제 Menu Sin-Integrate를 lick했을 때의 source code만 보기로 하자.

Private Sub mnuSinIn_Click()

변수들을 선언하고
Dim I, X1, Y1, X2, Y2 As Long
Dim Pi, DX1, DX2 As Double
Dim UniY As Double
Dim UniX, Sum As Double
Dim Min, Max As String

원주율 값을 준다.

Pi = 3.141592

다음으로 Y 축 중 X 축 상단에 있는 부분을 2/3 정도로 나누어 이 길이를 Y 축의 단위 길이 UniY로 한다.
UniY = (linXax.Y1 - linYax.Y1) / Pi

다음으로 X 축의 음의 부분의 길이를 p 로 하기 위해 UniX를 정한다.
UniX = linYax.X1 - linXax.X1

그 다음 Sum값을 0으로 초기화 한다.
Sum = 0#

그 다음 적분의 하한 값을 VB의 InputBox를 이용해 받아들인다.
Min = InputBox("하한 값은?(단 > - Pi) ")

또 적분의 상한 값을 VB의 InputBox를 이용해 받아들인다.

Max = InputBox("또 상한값은?(단 < 2*Pi 보다 큰값)")

하한 값을 그림에서 나타내기 위해  먼저 x축에서 Unit X twib 단위가 Pi로 scale한 것을 알아서 Min을 Pi로 나눈 다음 Unit X를 곱해주어
(UniX * Min/Pi) 위치를 정함. 그런데 x 축의 왼쪽 끝의 x 좌표 (linXax.X1)가 -Pi 자리 이므로 원점의 x 좌표는 linXax.X1+Unit x가 되므로
하한 값의 x좌표 X1은 결국
X1 = linXax.X1 + Int(UniX * (Min + Pi) / Pi)
와 같이 된다. 또 하한 값을 x 축위의 점으로 나타내면 그때의 Y좌표 Y1는 결국 x축의 Y좌표가 된다.
Y1 = linXax.Y1

또 우리는 적분을 Trapezoidal Rule로 할 것이므로 두 점씩 잡아 적분해야 하는데 처음 두 점의 왼쪽 점의 실제 X 좌표 DX1는 하한 Min값이다.
DX1 = Min

이제 상한과 하한을 등 간격으로 있는 2000 개의 점으로 나누어 각각 두점 씩 쌍을 이루어 Trapezoidal Rule로 적분하여
그결과를 다 더하기로 하자. 그러면 첫 번째 쌍의 왼쪽점의 좌표는 위에서 계산한 (X1,Y1)이 된다.

For I = 1 To 2000

첫 번째 쌍의 오른쪽 점의 그림을 그리기 위한 x 좌표 X2는 Min에서 (Max-Min)/2000=0.0005*(Max-Min)이 되므로 I=1일 때

X2 = Int(0.0005 * (Max - Min) * I / Pi * UniX)
X2 = X2 + Int(linXax.X1 + UniX * (Min + Pi) / Pi)

와 같이 될 것이다. 또 우리는 적분을 Trapezoidal Rule로 할 것이므로 두 점씩 잡아 적분해야 하는데 첫 번째 쌍의
오른 쪽 점의 X 좌표 DX2는

DX2 = I * 0.0005 * (Max - Min) + Min

와 같이 될 것이다. 또 그림 상에서 첫 번째 쌍의 오른쪽 점의 x값에 대응하는 sine 함수 값을 나타내는 Y2는

Y2 = linXax.Y1 - UniY * Sin(DX2)

와 같이 되어 결국은 첫 번째 쌍의 두점으로 사다리꼴 적분한 영역은 결국 (X1,Y1), (X2.Y2)를 대각선 끝점으로 하는 직사각형
비슷하므로 그 영역을 청색의 Box로 표시하는 code는

frmNuint.Line (X1, Y1)-(X2, linXax.Y1), RGB(0, 0, 255), B

와 같다.또 이 때의 적분 값은 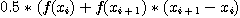이므로 이 값을 이 전까지의 적분 결과 값을 갖고 있는 sum에 더해 주면

Sum = Sum + (Sin(DX1) + Sin(DX2)) * 0.5 * (DX2 - DX1)

와 같이 된다.

다음 쌍의 적분을 위해 현재 쌍의 오른쪽 점을 다음 쌍의 왼쪽점으로 넘겨 주면
X1 = X2
Y1 = Y2
DX1 = DX2
가 되고 다음 쌍의 오른 쪽 점의 계산을 위해 Next I에 의해 For I = 1 To 2000 바로 밑으로 가서 계산을 하는 등 계산을 2000번 반복하면

Next I

적분의 결과가 sum에 있게 된다. 그런데 그냥 sum을 찍어라 하면 VB에서 소수점이하 몇 자리 까지 보여주어야 하는지 고민하므로 결과에 1000을 곱한 다음
Sum = 1000 * Sum
소수점이하를 버리고 (Int(Sum)) 다시 0.001을 곱하면 소수점이하 3 째자리 까지 정확히 볼 수 있다.
Sum = Int(Sum) * 0.001

그 결과를 lblresult의 Caption에 표시한다. (Str()함수는 VB에서 수를 문자열(string)로 표시해주는 함수이다.)

lblResult.Caption = "계산결과 " + Str(Sum)

End Sub

연습문제: mnuTaDisp_Click() procedure를 이용해 Tan 함수를 -Pi/2에서 Pi/2까지 그리고 이 구간에서 임의 구간을 적분하여 그 결과를 나타내는 프로그램을 작성하라.

4. Improper Intergral의 수치해석

   Improper Integral이란 적분 구간내에서 피적분 함수 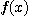가 발산하거나 또는 값을 갖지 않는 경우를 의미한다. Improper Intergral도 적분 가능한 또는 적분 값이 존재하는 Integrable Improper Integral이 있고 적분 불가능한 Improper Integral이 있다. 여기서는 Integrable Improper Integral을 수치 적분하는 방법에 관해 연구해 보자.
   적분 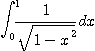은 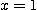에서 피적분 함수가 발산한다. 그러나 적분을 하면

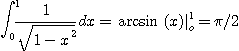
로 적분이 가능하므로 Integrable Improper Integral이다. 이에 비해 적분 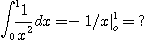이 되어 norintegrable Improper Integral이 된다.

  이제 Integrable Improper Integral 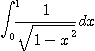수치 적분하는 방법에 관해 논의해 보기로 하자. 먼저 피적분 함수가 발산하는 주위에서는 적분을 해석적으로 정확히 하고 나머지 부분에서는 수치적분 하면 된다. 즉

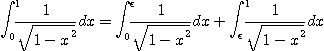
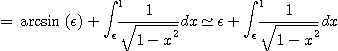
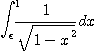이 된다. 따라서 을 점점 1에 접근 시키면서 을 Gaussian quadrature등으로 수치 적분하여 그 값에 을 더해 적분 값의 변화를 자기가 만족하는 범위내에서 변화하지 않으면 그 값을 적분 값을 택한다.

연습문제: 적분 1)

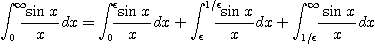
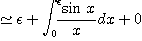
을 이용하여 이 적분값을 소수점 이하 3 자리까지 정확히 구하여 보라.

적분 2)

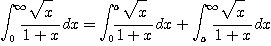
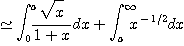
을 이용하여 이 적분값을 소수점 이하 3 자리까지 정확히 구하여 보라.

(Hint: 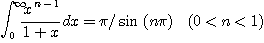)